泊松分布與輻射測量
泊松分布與輻射測量
江如秋
2022年7月
放射性衰變的泊松分布
放射性衰變是一個隨機過程,每秒衰變的次數稱為活度,通常以貝可(Becquerel)為單位,然而它只是一個平均值,實際衰變的次數一般會用泊松分布(Poisson distribution)描述。舉例說,1貝可的放射性銫-137在10秒內的衰變次數平均為10次,但實際上不同時候的衰變次數是以不同的機率出現(圖一),接近平均值的次數會有較高的機率出現,而遠離平均值的次數出現機率則會遞減。
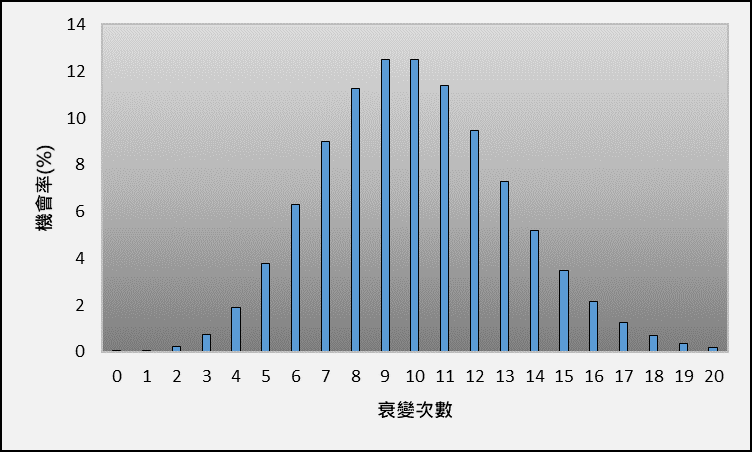
圖一 活度為1貝可的銫-137在10秒的衰變次數機率分布。
泊松分布的特性會為輻射測量帶來不同程度的不確定性。跟據圖一的分布,測量結果有機會是測出10次衰變,但亦有不少機會測得其他次數的衰變。在這個情況下,儘管探測器的能力有多好,測量結果仍存在不確定性。
如何減少測量的不確定性?
在統計學上,我們通常會利用標準差(standard deviation)去描述一個分布的擴散程度及釐定測量的不確定性。根據標準差的公式,泊松分布所衍生的不確定性與1/√N有關,當中N是探測器測得的信號次數。因此,當探測器測得的信號次數越多,不確定性則會減少,而延長測量時間是其中一個有效增加N的方法。圖二展示了測量時間對測量結果分布的影響。長時間測量結果分布顯得較為集中,不確定性較小。相反,短時間測量結果分布則較為分散,不確定性較大。
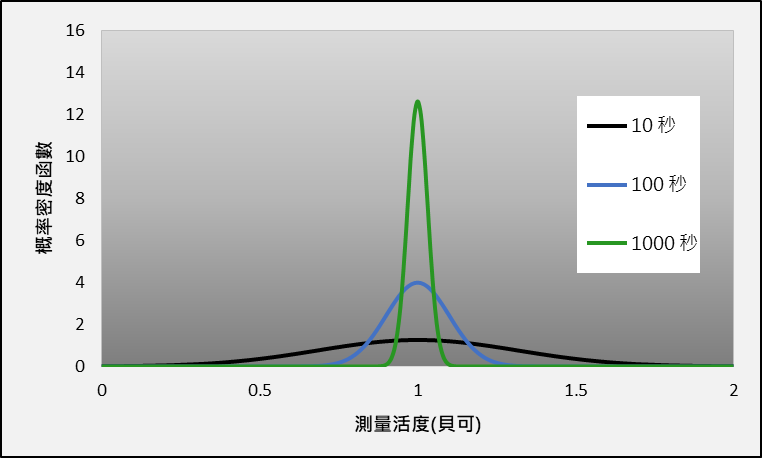
圖二 不同測量時間對測量結果分布的影響。(註:概率密度函數越大,代表測量活度出現在相應範圍的機率越高。)
測量時間與探測下限
香港天文台在環境輻射監測計劃中監測的核素活度水平頗低,所以實驗室必須對樣本進行長時間測量以增加探測器測得的信號次數,從而降低測量的不確定性。現實中,我們不可能無限延長測量時間來將測量不確定性降至零。當核素的活度低於某個水平,長時間測量也不足以有效地降低其測量的不確定性,導致測量結果不能與由電子雜訊及本底輻射所引致的信號區分時,該水平便是探測器的探測下限。