泊松分布与辐射测量
泊松分布与辐射测量
江如秋
2022年7月
放射性衰变的泊松分布
放射性衰变是一个随机过程,每秒衰变的次数称为活度,通常以贝可(Becquerel)为单位,然而它只是一个平均值,实际衰变的次数一般会用泊松分布(Poisson distribution)描述。举例说,1贝可的放射性铯-137在10秒内的衰变次数平均为10次,但实际上不同时候的衰变次数是以不同的机率出现(图一),接近平均值的次数会有较高的机率出现,而远离平均值的次数出现机率则会递减。
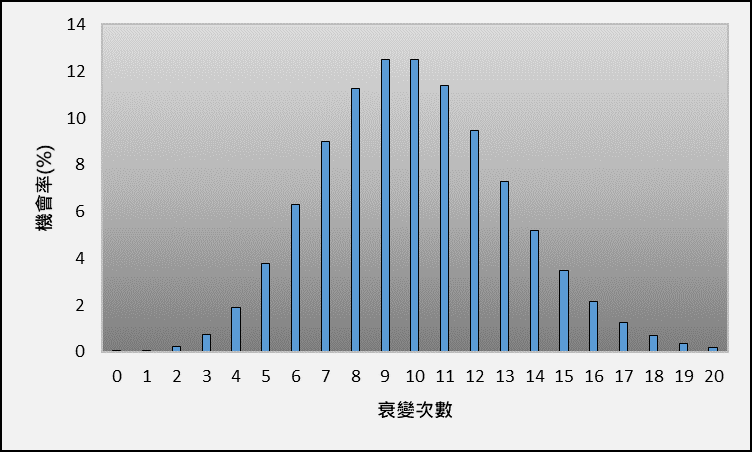
图一 活度为1贝可的铯-137在10秒的衰变次数机率分布。
泊松分布的特性会为辐射测量带来不同程度的不确定性。跟据图一的分布,测量结果有机会是测出10次衰变,但亦有不少机会测得其他次数的衰变。在这个情况下,尽管探测器的能力有多好,测量结果仍存在不确定性。
如何减少测量的不确定性?
在统计学上,我们通常会利用标准差(standard deviation)去描述一个分布的扩散程度及厘定测量的不确定性。根据标准差的公式,泊松分布所衍生的不确定性与1/√N有关,当中N是探测器测得的信号次数。因此,当探测器测得的信号次数越多,不确定性则会减少,而延长测量时间是其中一个有效增加N的方法。图二展示了测量时间对测量结果分布的影响。长时间测量结果分布显得较为集中,不确定性较小。相反,短时间测量结果分布则较为分散,不确定性较大。
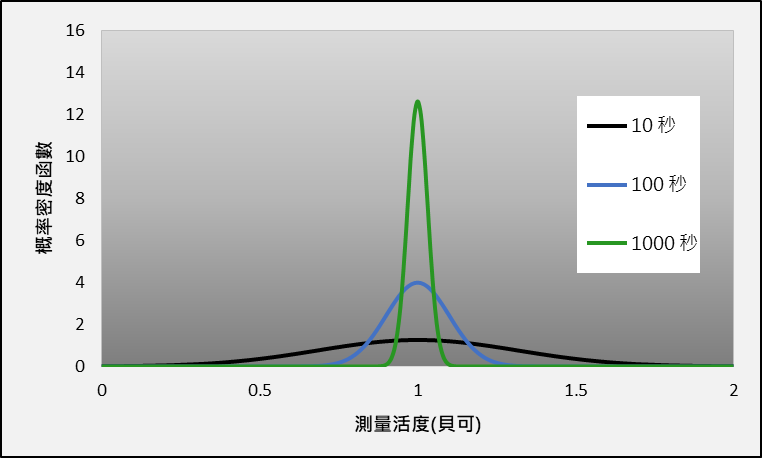
图二 不同测量时间对测量结果分布的影响。(注:概率密度函数越大,代表测量活度出现在相应范围的机率越高。)
测量时间与探测下限
香港天文台在环境辐射监测计划中监测的核素活度水平颇低,所以实验室必须对样本进行长时间测量以增加探测器测得的信号次数,从而降低测量的不确定性。现实中,我们不可能无限延长测量时间来将测量不确定性降至零。当核素的活度低于某个水平,长时间测量也不足以有效地降低其测量的不确定性,导致测量结果不能与由电子杂讯及本底辐射所引致的信号区分时,该水平便是探测器的探测下限。